Research topics

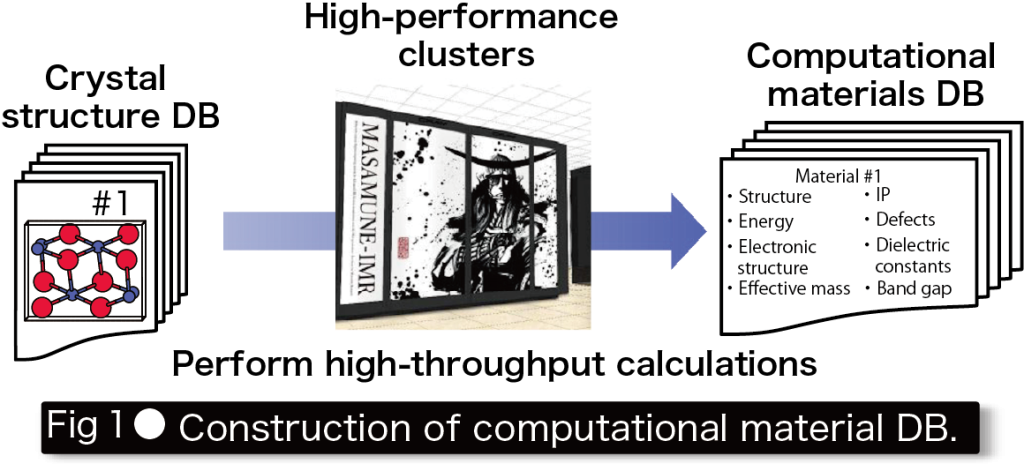
Conventional materials research has been experiment-driven, and new materials have been discovered through repeated hypothesis testing. However, the experimental process involving synthesis and measurement requires a large number of funds and human capital and significantly restricts development speed. On the other hand, computing power, following Moore’s law, has advanced remarkably with tremendous exponential growth, and as a result, first-principles calculations that predict physical properties based on quantum mechanics can now be used in materials research. More recently, it has become possible to perform first-principles calculations on several hundred thousand materials and to compile a database (DB) of the properties obtained(Fig. 1). Thus, we are entering the era of big data in materials science.
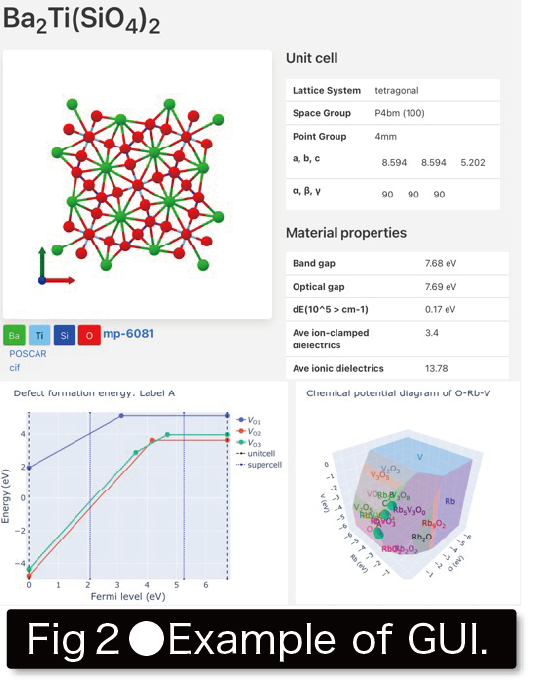
These computational materials DB has many applications, such as “selection of the best materials for each application from among previously reported materials," “use as training data for machine learning (ML)," and “discovery of materials that show unique physical and chemical trends from among many materials. This research group aims to discover innovative new materials and elucidate the origin of physical properties appearing in textbooks by constructing and applying the fundamental technologies necessary for computational materials DB(Fig. 2).

Many point defects such as vacancies and impurity elements exist in materials and play important roles in material functions. For example, p-type GaN was realized by adding a small amount of Mg. Also, in the anode material of the Li-ion conductor, it is necessary to introduce a large amount of Li vacancies for Li diffusion. However, it is extremely difficult to perform the atomic-level analysis necessary to investigate point defect properties in detail by experiment alone. Therefore, since around 2000, first-principles calculations have been used to investigate point defect properties.

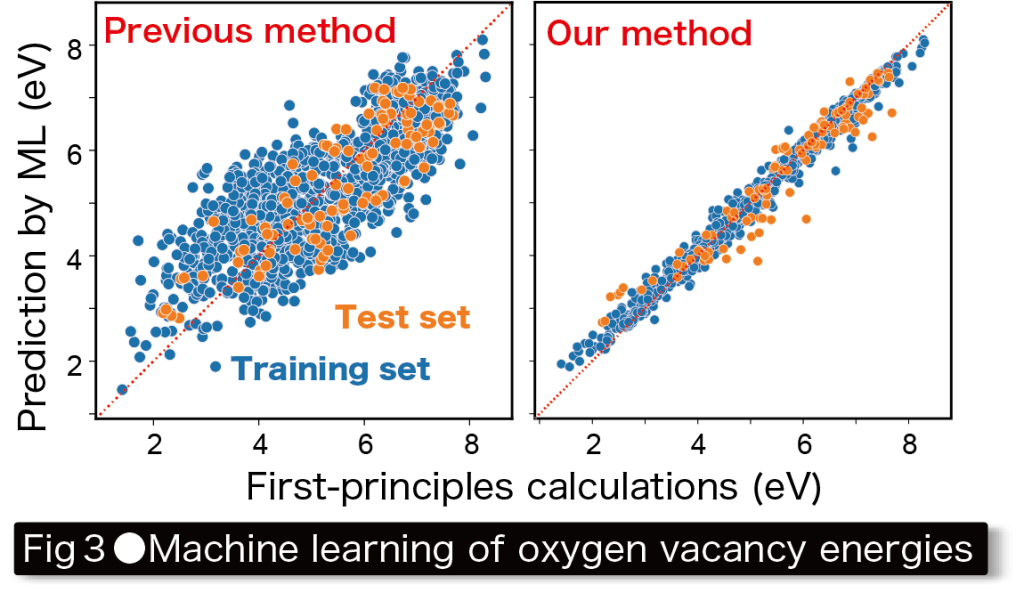
We have developed methods to precisely calculate the formation energies of point defects and transition energies associated with absorption and emission, as well as programs to automate complex point defect calculations and have applied these methods to various materials. We recently performed systematic calculations on oxygen vacancies in ~1,000 oxides and machine learning their vacancy formation energies using the above-mentioned computational materials database development program(Fig. 3).

In recent years, two-dimensional semiconductors have been actively studied to overcome Moore’s law and further improve the integration of next-generation semiconductor devices. Among these materials, transition metal dichalcogenides are expected to have a wide range of applications in two-dimensional electronic devices because of their excellent carrier mobility and insulating properties.
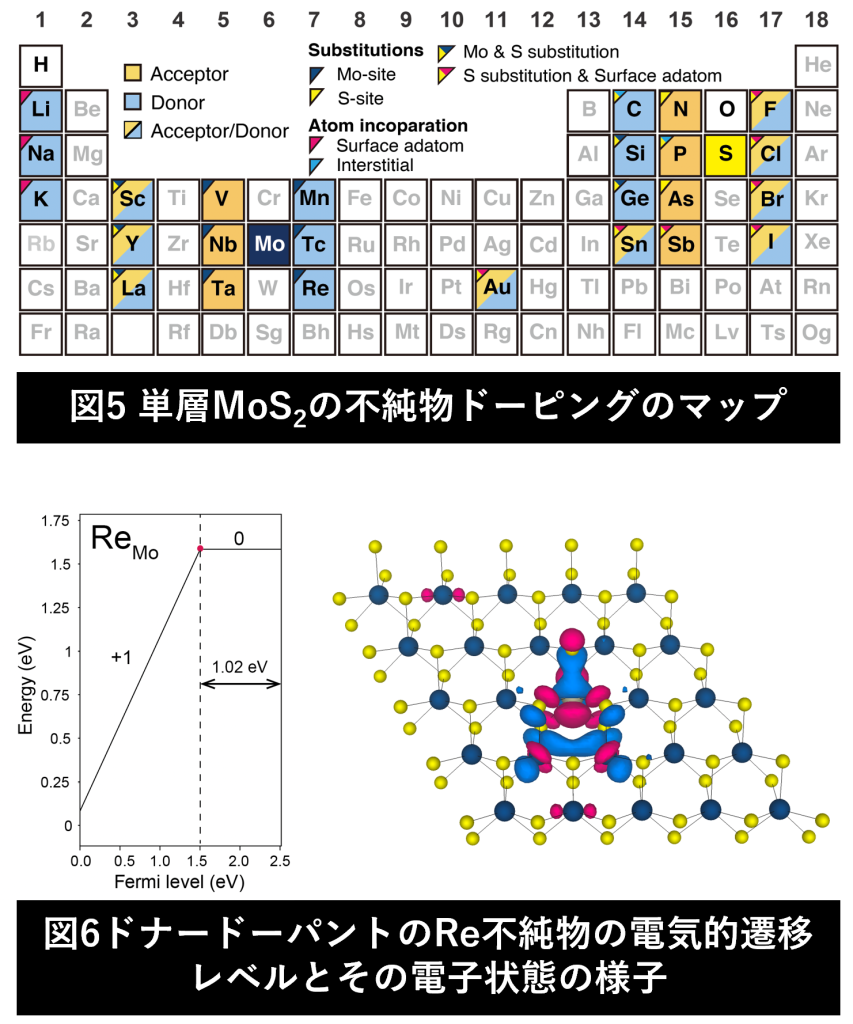
In semiconductors, physical properties can be controlled by doping. It is no exaggeration to say that “what elements are doped at which sites" determines the physical properties of semiconductors (Figure 5). First-principles calculations can be used to calculate the electronic states of doped materials (Figure 6). We are exploring effective impurity doping methods for two-dimensional semiconductors, mainly transition metal dichalcogenides, using first-principles calculations, with the aim of realizing next-generation two-dimensional devices.

Due to its large discharge capacity and abundance in the earth’s crust, Mg is attracting attention as a next-generation secondary battery material. Cathode materials with high discharge capacity, high operating voltage, structural stability, and high ionic conductivity are essential for the realization of Mg secondary batteries. However, since Mg is a divalent ion with a large ionic radius, it has a strong affinity to the matrix, which is known to have a negative effect on structural stability and ionic conductivity. We are attempting to elucidate the ionic conduction mechanism using a high-throughput flow as shown in Fig. 7. Furthermore, we are searching for new cathode materials with high structural stability and ionic conductivity by doping impurities.